Restricting a set of paths to just the unique longest paths that contain them all
Before trying the code in this section, make sure that you have created the "edges" table (see cr-edges.sql) and installed all the code shown in the section Common code for traversing all kinds of graph.
Start by defining an example undirected cyclic graph and by computing all the paths from a selected start node:
delete from edges;
alter table edges drop constraint if exists edges_chk cascade;
alter table edges add constraint edges_chk check(node_1 <> node_2);
insert into edges(node_1, node_2) values
('n01', 'n02'),
('n02', 'n03'),
('n03', 'n04'),
('n04', 'n05'),
('n05', 'n06'),
('n06', 'n07'),
('n07', 'n08'),
('n01', 'n09'),
('n09', 'n05'),
('n05', 'n10'),
('n10', 'n08');
-- Implement the denormalization.
insert into edges(node_1, node_2)
select node_2 as node_1, node_1 as node_2
from edges;
Re-create the simpler implementation of "find_paths()" that implements the cycle prevention code, shown at cr-find-paths-with-nocycle-check.sql. Now generate the paths that start at the node "n01", restrict these to just the shortest paths, and restrict these further to the set of longest unique containing paths:
call find_paths(start_node => 'n01');
call restrict_to_shortest_paths('raw_paths', 'temp_paths');
call restrict_to_unq_containing_paths('temp_paths', 'unq_containing_paths');
\t on
select t from list_paths('unq_containing_paths');
\t off
This is the result:
path # cardinality path
------ ----------- ----
1 4 n01 > n02 > n03 > n04
2 5 n01 > n09 > n05 > n06 > n07
3 5 n01 > n09 > n05 > n10 > n08
These are the unique containing paths of the shortest paths from the raw paths. Here they are. The pictures are numbered with the value assigned by row_number() (see the implementation of "list_paths()"):
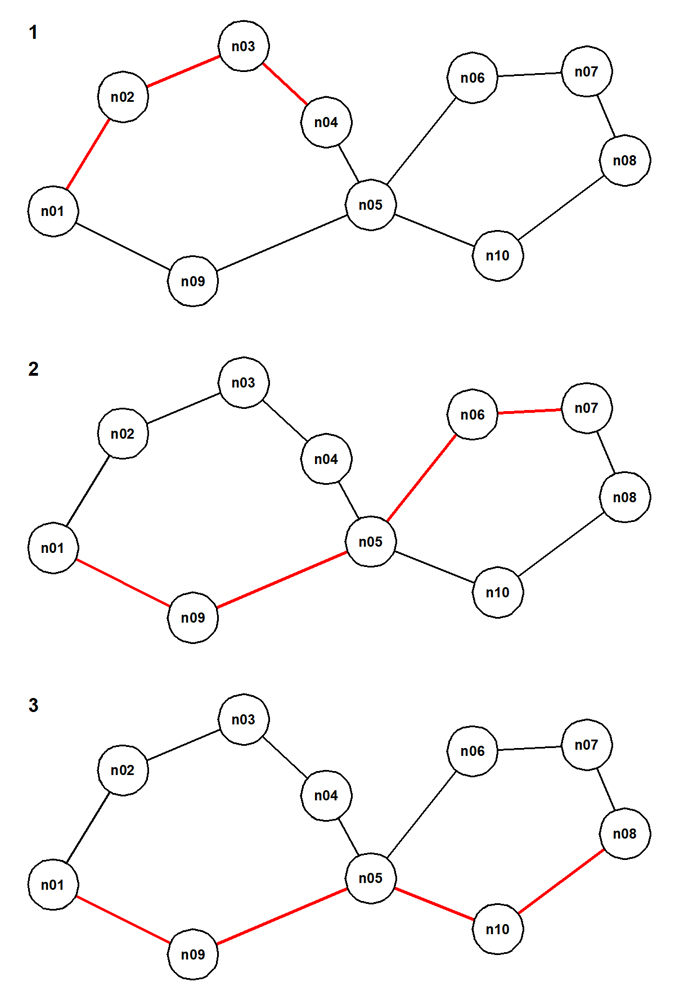
For contrast, do this:
call restrict_to_unq_containing_paths('raw_paths', 'temp_paths');
call restrict_to_longest_paths('temp_paths', 'unq_containing_paths');
\t on
select t from list_paths('unq_containing_paths');
\t off
This is the result:
path # cardinality path
------ ----------- ----
1 6 n01 > n02 > n03 > n04 > n05 > n09
2 6 n01 > n09 > n05 > n04 > n03 > n02
3 9 n01 > n02 > n03 > n04 > n05 > n06 > n07 > n08 > n10
4 9 n01 > n02 > n03 > n04 > n05 > n10 > n08 > n07 > n06
These are longest paths from the unique containing paths of the raw paths. Here they are. The pictures are again numbered with the value assigned by row_number().
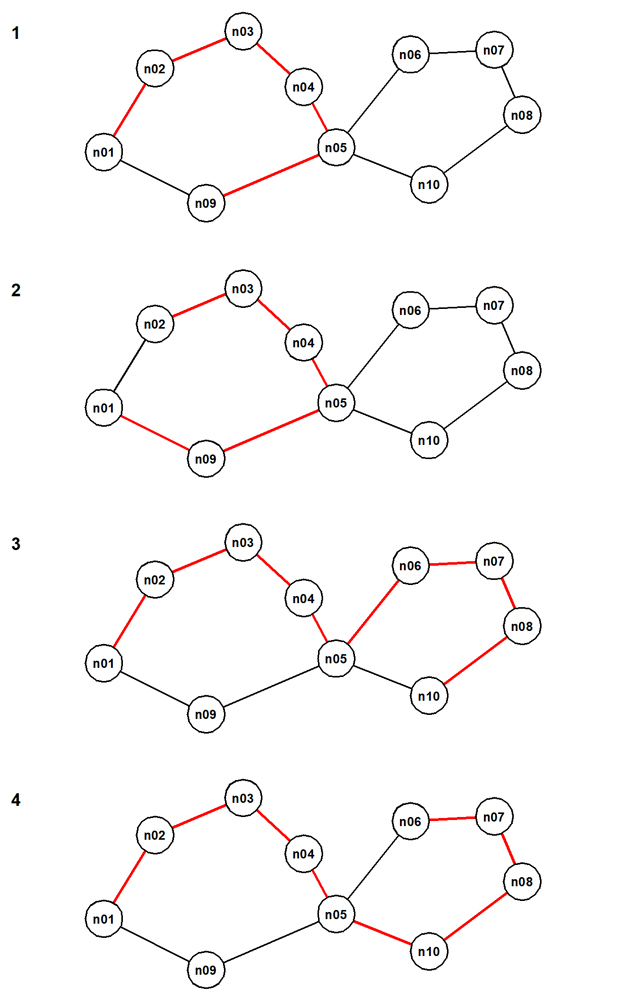
These two pictures together provide a very compact way to understand the meaning of the set of twenty-six distinct raw paths produced by call find_paths(start_node=>'n01').